How to Differentiate Math Instruction (Without the Stress of Creating New Resources)

Differentiating math instruction can often feel like just another thing on your already full plate. You may believe you don’t have time to differentiate—or maybe you think you can’t make it work with the resources you have. But here’s the truth: you probably already differentiate more than you realize.

You don’t need to create brand-new lessons from scratch to meet your students’ needs. And according to Westman (2020), “[Differentiating instruction] may be the single most important instructional move right now.” In today’s classrooms, we must explore and reflect on student needs, then adjust instruction in ways that build confidence and support achievement.

Let’s dive into five practical ways you can do just that.

1. Provide Open-Ended Activities

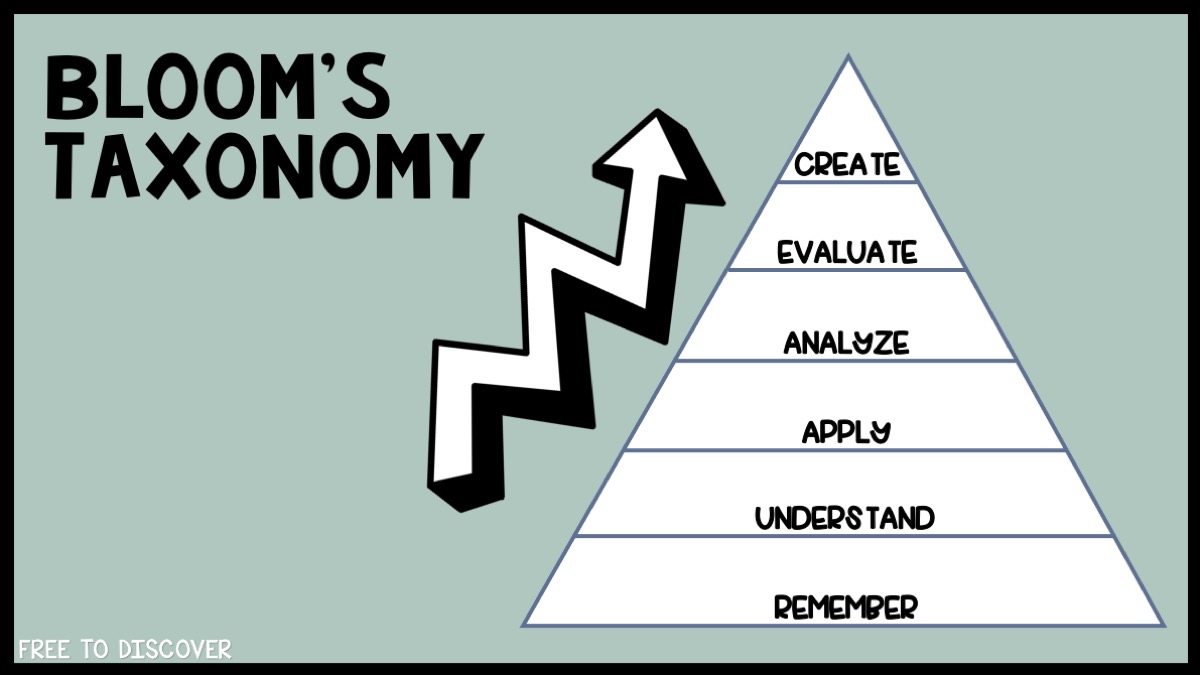
When planning activities, consider Bloom’s Taxonomy. Assigning tasks that involve remembering and understanding is an important foundation, but we shouldn’t stop there.

Examples of open-ended prompts:

• Create an expression with set parameters. For example, create an expression with at least three terms that simplifies to 2x+5. Want to differentiate? Add a requirement that at least one term must be a fraction or increase the minimum number of terms mandated.

• Select an equation that doesn’t belong with the others and justify why. What I love most about these types of questions is that there doesn't have to be a right answer! Is the solution to one different than the others? Does one only include integers? Engage in dialogue with students.

•  Develop and test a conjecture about a pattern. Pose a question like, "What do you notice about the pattern 7, 14, 21, 28, ...?" Some students will notice multiples of 7. Others will note that the numbers alternate between odd and even. Others may say the numbers are all divisible by 7. When else are these statements true? How would this be different if the list included multiples of 6?

Because of the “wiggle room” built into these activities, students naturally self-differentiate. Some may write a basic expression, while others push themselves to create something more complex. The same goes for justifying “which doesn’t belong”—as long as their reasoning is sound, their answer is valid.

This flexibility frees students to think deeply without being boxed in by a single correct answer, helping them climb Bloom’s ladder over time.

2. Give Students Choices

Choice is a powerful motivator. Even something as simple as offering two versions of a worksheet can make a big difference.

Example: After teaching simplifying algebraic expressions, you might create:

• Version A: Positive numbers only, so students can focus on distributing and combining like terms without the barrier of integers.

• Version B: Includes negatives for students ready for an extra challenge.

With some coaching, students learn to pick the version that best matches where they are in their learning journey.

I've used this strategy many times and where I find the resources to use varies: print resources from supplemental workbooks, worksheets from online searches, web tools such as Kuta Software, and Free to Discover differentiated math worksheets.

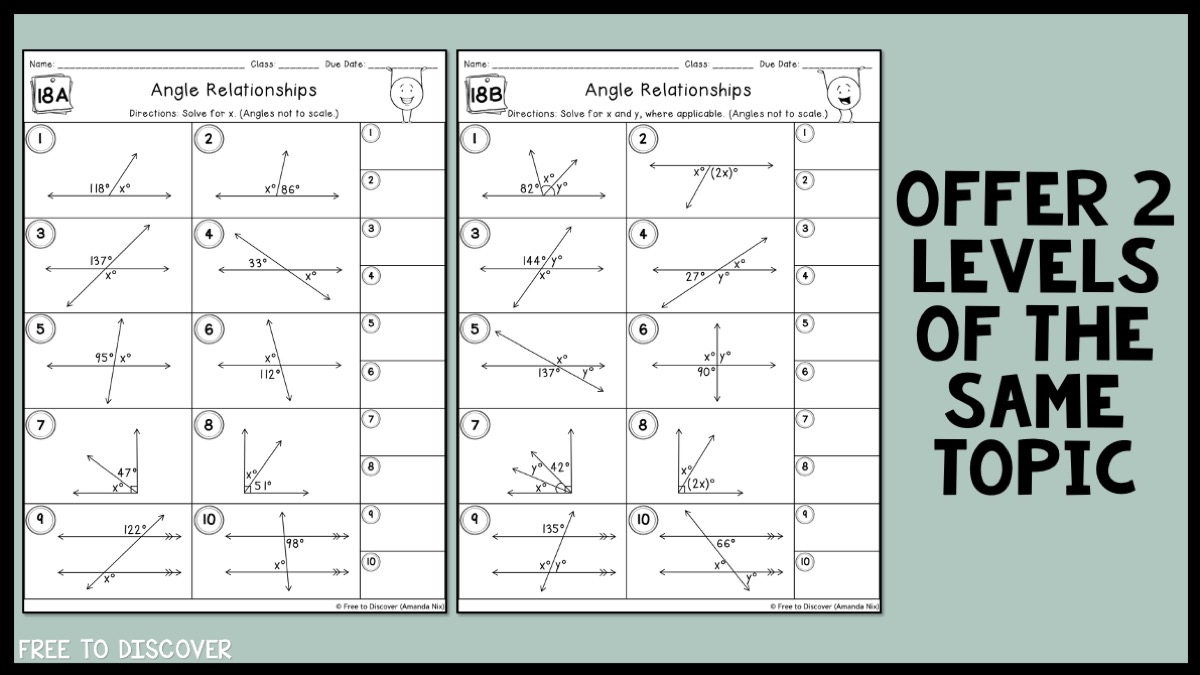
The worksheets pictured above are from the 8th Grade Math Skill Drills Companion Set.

3. Use Worksheet Generators Like Kuta

Sometimes you just need quick, no-frills practice problems. Tools like Kuta Software are great for that—they can instantly generate worksheets at different levels, saving you the time of writing new problems from scratch.

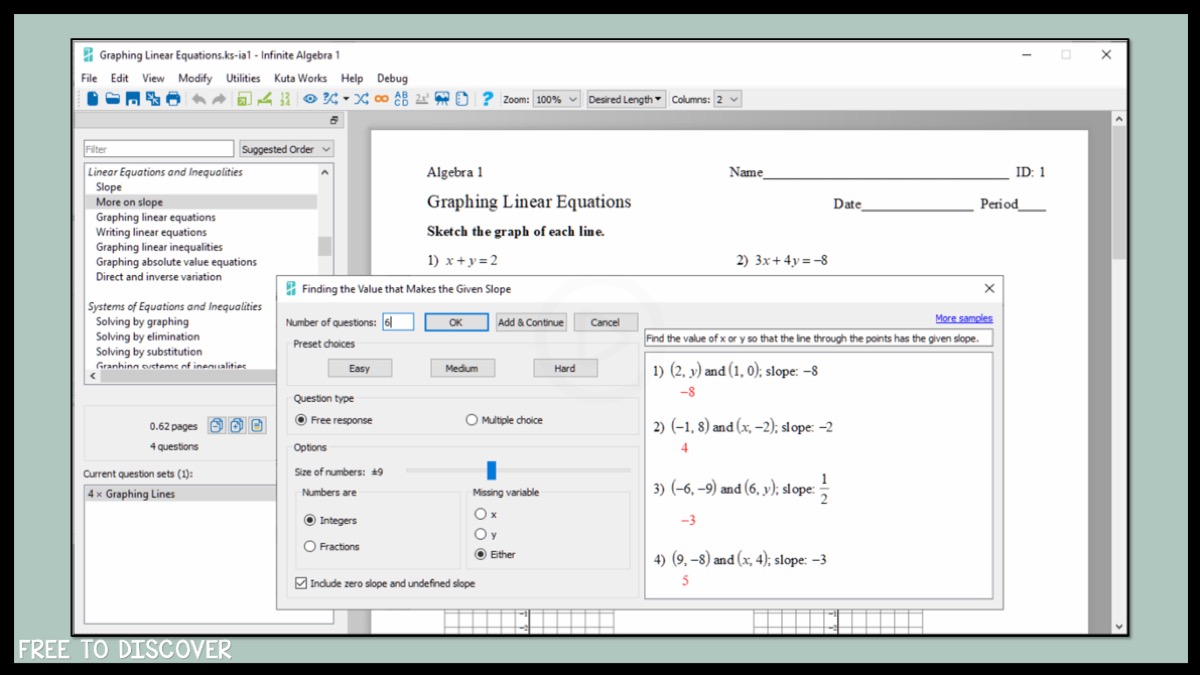
For example, you might:

• Print a two-step equations worksheet for students who are just getting started.

• Offer a multi-step equations worksheet to students who are ready for a challenge.

• Use a “Level Up” strategy where students start simple and move on only after showing mastery.

In the "Level Up" strategy, all students start with the simpler worksheet. Some students will continue to work only on this practice throughout the remainder of the time. Other students may choose to level up. If they get 5 problems correct in a row, they may choose to level up and move on to the more challenging problems. Advanced Strategy: Have multiple levels available so students can continue to level up more than once.

⚠️ The trade-off of online tools and AI sources? These generators give you volume, but the problems are typically straightforward drill. They don’t provide the scaffolds or built-in supports that some students need to be successful. They may not offer the variety of problems, formats, and numbers that would be valuable practice for your students.

4. Vary Levels of Support

Whole-class instruction is enough for many students—but not all. For students who need more, pull a small group to continue the lesson with added scaffolds.

This might mean:

• Using manipulatives for hands-on, concrete learning

• Drawing models or diagrams to aid visual learners

• Breaking problems into smaller steps and using checklists

As soon as they hit their “aha” moment, send them back to rejoin the class. This flexible support helps you meet diverse needs without rewriting your entire lesson plan.

5. Try Ready-to-Go Differentiated Notes & Practice

One of the simplest ways to differentiate is to start with resources already designed to meet a range of learners. That’s why I created my Differentiated Notes and Practice Worksheets—they’re structured to give every student an entry point while still challenging those who are ready for more.

Here’s what’s included:

Differentiated Notes

• Traditional Notes – Skeletal notes where students fill in examples with you, then try similar problems independently.

• Modified Notes – All examples are filled in, with only the practice problems left blank. Great for students who need less writing or have accommodations (IEPs, 504s, etc.).

• Teacher Notes – Fully completed notes for your reference or for students who were absent.

Differentiated Practice (Homework)

• Advanced Practice – Designed for high-flyers. Some problems may overlap with the basic set, but additional advanced problems are included for a deeper challenge.

• Basic Practice – The core assignment most students will complete at grade level.

• Modified Practice – A shortened version of the basic set, perfect for students who need fewer problems.

With these ready-to-go resources, you can spend less time creating multiple versions of assignments and more time teaching, supporting, and encouraging your students.

Wrapping It Up

Differentiation doesn’t have to be overwhelming. Remember, you can:

• Ask open-ended questions.

• Give students choices.

• Use worksheet generators and online tools.

• Scaffold with targeted support.

• Lean on differentiated notes and practice that are already built for multiple levels of learning.

Small adjustments to your teaching like these make a big impact. Students feel supported, challenged, and confident—and you don’t have to reinvent the wheel to get there.

👉 Want to see how differentiated notes and practice could save you planning time? Browse Differentiated Notes and Practice Worksheets on TPT.